
Hannemands teoriside
MATEMATIK
4-6. klasse
Et positionssystem er et talsystem, hvor cifrenes værdi afhænger af deres placering/position i tallet.

Ciffer
I Danmark bruger vi et talsystem, som består af 10 cifre/talsymboler.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Med disse 10 cifre kan du lave ALLE tal.
Tal
Et tal består altså af et eller flere cifre.
EKS: Tallet 17 består af to cifre, nemlig 1 og 7.
Tallet 193 består af cifrene 1, 9 og 3.
Titalssystemet
Vi kalder vores positionssystem for titalssystemet, fordi grundtallet er 10.
10 = 10 enere
100 = 10 tiere
1000 = 10 hundreder
Sammentrukket form
Udvidet form
8436
8000+400+30+6 = 8436
8000
400
30
6
8436
XXXX
xx
2

Tusindtalsseparator
En tusindtalsseparator bruges til at gøre store tal lettere at læse ved at opdele dem i grupper af tre cifre – startende fra højre. Man kan enten bruge mellemrum eller punktum.
EKS:
8 436
1 245 534
eller
8.436
eller
1.245.534

Sætte separator:
Start fra højre i tallet.
Sæt et punktum efter hvert tredje ciffer.
Hvis det er et decimaltal gælder det kun foran kommaet, ikke efter.
BEMÆRK: På engelsk (og i fx USA) bruges typisk komma (,) som tusindtalsseparator, fx 1,000,000 og punktum som komma.

3
Negative tal er mindre end nul.
Negative tal har et minus foran (fortegn) fx. -7.
Når man bruger et minustegnet til at vise, at et tal er negativt, kalder man det for et fortegn

Negative tal
Positive tal
På en tallinje er:
-
de negative tal placeret til venstre for 0.
-
de positive tal er placeret til højre for 0.
Et positivt tal har et plustegn (+) som fortegn, men hvis der ikke er sat et fortegn, er tallet oftest positivt.
Brug af negative tal
Brug af negative tal
Brug af negative tal
Brug af negative tal
4
Plus og minus på tallinje
Du kan bruge en tallinje, når du skal regne med negative tal.
Når vi lægger noget til (adderer, +), bevæger vi os til højre på tallinjen, og når vi trækker noget fra (subtraherer, -), bevæger vi os til venstre.
1)
10 – 7 = 3
Du har 10 kr. i din pung,
men skylder 7 kr. væk.
10 – 7 = 3
=
Du skylder 7 kr. væk,
men har 10 kr. i din pung.
–7 + 10 = 3
2)

1)

2)
Plus og minus, samle og forenkle
Når der er flere positive og negative tal i et regnestykke, kan det være lettere først at samle alle negative tal og alle positive tal i hver deres bunke.
Strategi: Sæt cirkel om tallet og dets regnetegnet.

Faktorernes orden er ligegyldig i plus og minus
Regn med negative tal på tallinje - let
5
Fortegn og regnetegn
Symbolerne + og - bruges som regnetegn (grøn) og som fortegn (blå)
Fortegn (+, -) viser om tallet er positivt (+5) eller negativt (-5).
Et fortegn knytter sig kun til ét bestemt tal. Tit er plus-fortegn underforstået (5 = +5).
Regnetegn (+, -, ・, :, potens, kvadratrod) viser hvad du skal gøre med de tal, der indgår i regnestykkerne.
Ofte sætter man med et minus-fortegn i parentes for ikke at forveksle fortegn og regnetegn.
4 + (–1) – (+3)
4 – (– 5)
For at kende forskel sættes nogle gange en parentes omkring fortegn.
Fortegnsregler for gange og division
Fortegnsreglen, der handler om, hvordan vi gør, når vi ganger og dividerer to tal.
Gange
Dividere

Har tallene ens fortegn, fås et positivt resultat.
Har tallene to forskellige fortegn, fås et negativt resultat.
EKS:
Hvis du har lånt 5 kr. af hver af dine 3 venner, hvor mange penge skylder du så væk? Svar: Du skylder 15 kr.
(–5) • 3 = - 15
EKS:
Du køber busbilletter til dig selv og 4 af dine venner. Du lægger ud for alle og betaler i alt 65 kr. Hvor meget skylder dine venner dig for busbilletten?
–65 : 5 = -13
Parentesregler
"At hæve en parentes" er det udtryk, vi bruger, når vi fjerner en parentes.
Hvis der står plus foran parentesen, kan vi bare fjerne den.
Hvis der står der minus foran parentesen, skal vi ændre alle tegn inde i
parentesen. Det betyder, at plus ændres til minus og omvendt minus til plus.
EKS:
Plusparentes
7 + (3 - 5) = 7 + 3 – 5 = 5
Minusparentes
8 – (2 + 5) = 8 – 2 – 5 = 1
Hvis der ikke står et fortegn foran et tal, så er det positivt (+).
Eks 2 = +2
a – (b + c) = a – b – c
a + (b + c) = a + b + c
6
7-9. kl
Plusse
At plusse (addere) to tal er det samme som at se, hvor meget de er tilsammen.
Hvis du f.eks. har 10 kr. i din pung, men du skylder 7 kr. væk, så har du kun 3 kr. til dig selv. Matematisk ser det således ud:
EKS:
10 + (-7) = 10 - 7 = 3
At lægge -7 til, er altså det samme som at trække 7 fra.
EKSEMPLER:
4 + (+8) = 4 + 8 = 12
4 + (-8) = 4 - 8 = - 4
Minus
At minus (subtrahere) et tal fra et andet er at se hvor stor forskel, der er på de to tal.
Hvis et fly befinder sig i 150 meters højde, og flyver over en sø, der er 50 meter dyb, så er afstanden fra flyet til søbunden 200 meter. Matematisk ser det således ud:
EKS:
150 − (−50) = 150 + 50 = 200
At trække -50 fra er altså det samme som at lægge 50 til.
EKSEMPLER:
4 - (+8) = 4 - 8 = - 4
4 - (-8) = 4 + 8 = 12
Gange og dividere
Fortegnsregler
Gange
EKSEMPLER:
(-4) • 8 = - 4 • 8 = - 32
(+4) • (-8) = 4 • - 8 = - 32
(-4) • (-8) = - 4 • - 8 = 32


Dividere

Lommeregner
Hvis du bruger lommeregner til at regne med negative tal, skal du huske at taste fortegnet. Knappen kan se sådan ud:
(-) +/-
Regn med negative tal på tallinje - pilens retning
Regn med negative tal
- fortegn og regnetegn
a + (+ b) = a + b
a + (– b) = a – b
a – (+ b) = a - b
a – (– b) = a + b
(–a)・b = –ab
a・(–b) = –ab
(–a)・(–b) = ab
Regn med negative tal
- gange og dividere

7
Potenser er tal skrevet på en speciel måde.

Eksponenten viser, hvor mange gange grundtallet skal ganges med sig selv.
Grundtallet kaldes også basen eller roden.
3
2 = 2 • 2 • 2 = 8
EKS:
Læses 2 i tredje
2 betyder, at tallet 2 skal ganges med sig selv 3 gange.
3
Fra potens til gangestykke
Hvis du skal finde resultatet af en potens, kan du omskrive til et gangestykke og regne det.
EKS:
8
1
= 8
5
2
= 5 • 5 = 25
3
4
= 3 • 3 • 3 • 3 = 81
4
5
= 4 • 4 • 4 • 4 • 4 = 1024
Otte i første
Fem i anden
Tre i fjerde
Fire i femte
Fra gangestykke til potens
Modsat kan du skrive gangestykker, hvor det samme tal bliver ganget flere gange, på en lettere og kortere måde.
EKS:
7
3
7 • 7 • 7 =
8 • 8 • 8 • 8 • 8 • 8 • 8 =
8
7
a⁰
Det gælder også for potenser, at:

Man kalder det også 2 opløftet til tredje potens
a = a • a • a • a • a
Et tal i nulte er altid 1.
8 opløftet til første potens
5 opløftet til anden potens
3 opløftet til fjerde potens
4 opløftet til femte potens
Bevis
8
Potenser med roden 10, kaldes tierpotenser.
Man bruger tierpotenser til at skrive enten meget store eller meget små tal på en kortere måde.
Store tal

EKS:

Eksponenten fortæller hvor mange nuller, der kommer efter et-tallet.
Hér 6 nuller
Små tal


Et-tallet skal stå på denne plads efter komma.
Hér plads nr. 6
Den videnskabelige skrivemåde
Forklaring
5.000.000.000 kan skrives:

0,000001 kan skrives:
Eksempler på afstand til solen eller lysets hastighed
Tierpotenser er også brugbare, når man skal sammenligne meget små eller store tal.


Tallet i eksponenten svarer til antal decimaler.
Tierpotenser, oversigt

9
7-9. kl
Regneregler for potens med samme rod
Gange
Man ganger to potenser med samme rod ved at beholde grundtallet og plusse eksponenterne.
EKS:
Dividere
Man dividerer to potenser med samme rod ved at beholde grundtallet og minus eksponenterne.
måske skal dividere vises på brøk

Regneregler for potens med samme eksponent
Gange
Man ganger to potenser med samme grundtal ved at beholde grundtallet og plusse eksponenterne.
Dividere
Man dividerer to potenser med samme eksponent ved at dividere de to grundtal.

Potens til ny potens
Man opløfter en potens til ny potens ved at gange eksponenterne og beholde grundtallet.

Potens med negativt grundtal
En potens, hvor grundtallet er negativt, ser sådan ud:

Man skal gange -2 med sig selv. Minus gange med minus giver et positivt resultat.

Generelt gælder det at:
-
Hvis grundtallet er et negativt tal og eksponenten er et lige tal, så bliver facit et positivt tal.
-
Hvis grundtallet er et negativt tal og eksponenten er et ulige tal, så bliver facit et negativt tal.
VIGTIGT!


og
=

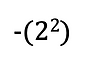
er ikke det samme
Sammenligning:

Her er det hele tallet - 2, der opløftes i anden.

Her er det 2 tallet, der opløftes i anden. Minustegnet står udenfor.
Potens med negativ eksponent
En potens, hvor eksponenten er negativ, ser sådan ud:

Vi kan finde resultatet ved at lave potensen om til en brøk. Her sættes 1 i tælleren og potensen i nævneren men med omvendt fortegn i eksponenten.

Men hvorfor hænger det sådan sammen?

Man kan trække den ene eksponent fra den anden, når grundtallene er de samme. Hvis vi forestiller os et regnestykke, hvor den første eksponent derfor er mindre end den anden eksponent, vil vi ende med en negativ eksponent.

Vi kan forkorte brøken. Potenserne viser som bekendt vores grundtal ganget med sig selv et bestemt antal gange, så vi kan ligeledes dividere med grundtallet flere gange.

Vi har nu beregnet brøken/divisionsstykket på to måder, og sådan har vi vist, at de to resultater giver det samme:




10
Rødder
Rødder betyder, at man skal finde det tal, som ganget et bestemt antal gange giver den værdi, der står under rodtegnet.

2 er antallet af gange et tal skal ganges med sig selv for at få 9.
Bemærk, at kvadratroden almindeligvis ikke har et 2-tal stående på rodeksponentens plads.


fordi
3 ganget med sig selv 2 gange er 9


fordi
3 ganget med sig selv gange er 9


3 ganget med sig selv 4 gange er 81
fordi
Stil spørgsmålet: Hvilket tal ganget med sig selv to gange giver 9?
Stil spørgsmålet: Hvilket tal ganget med sig selv tre gange giver 27?
Stil spørgsmålet: Hvilket tal ganget med sig selv fire gange giver 81?
Ofte vil man kun skulle arbejde med enten kvadratroden eller kubikroden.
Kvadratrod
Kvadratroden af et tal er det positive tal, der ganget med sig selv to gange giver tallet (under rodtegnet).
Kvadratroden af 9 er 3 fordi


Kvadratroden er altså det modsatte af at sætte noget i anden potens.
Der findes kvadratrødder, som ikke kan beskrives med et bestemt brøktal eller decimaltal. Det betyder, at man oftest er nødt til at afrunde det tal, man får på lommeregnere eller i regnearket.

Kubikrod
Kubikroden af et tal er det tal, der ganget med sig selv tre gange giver tallet (under rodtegnet).

Kubikroden af 8 er 3 fordi


Kubikroden er altså det modsatte af at sætte noget i tredje potens.

n er antallet af gange et tal skal ganges med sig selv for at få a.
Kvadratroden af 9
Kubikroden af 27
Den fjerde rod af 81
Tallet kan ikke være negativt, da der ikke er noget tal, der ganget med sig selv giver et negativt resultat.
Tallet må gerne være negativt.
11
Sammenhæng mellen rod og potens
Der en sammenhæng mellem rødder og potenser, nemlig at de er hinandens modsatte funktioner. Når man løfter et tal i anden potens og derefter finder kvadratroden af det, er man tilbage ved sit grundtal i potensen. Det samme gælder, når man løfter et tal i tredje potens og derefter finder kubikroden af det.

Anden potens er det modsatte af kvadratrod.
Tredje potens er det modsatte af kubikrod.
Fjerde potens er det modsatte af den fjerde rod.
n´te potens er det modsatte af den n´te rod.
Dette gælder for positive tal.
Bemærk, at kvadratroden almindeligvis ikke har et 2-tal stående på rodeksponentens plads.
12
7-9. kl
Regneregler for rødder med samme rodeksponent
Gange
Man ganger to rødder, der har samme rodeksponent, ved at gange de to radikander med hinanden.

Dividere
Man dividerer to rødder, der har samme rodeksponent, ved at dividere de to radikander med hinanden.

Regneregler for rødder med samme radikand
Gange
Man ganger to rødder, der har samme radikand, ved at gange de to rodeksponenter og opløfte radikanden i summen af de to rodeksponenter.

Dividere
Man dividerer to rødder, der har samme radikand, ved at gange de to rodeksponenter og opløfte radikanden i differencen af de to rodeksponenter.

Rod med negativ radikand
Det kun muligt at tage roden af et negativt tal, hvis rodeksponenten er et ulige tal.
Både 2² og (-2)² giver 4. Men når vi tager kvadratroden af 4, vil vi imidlertid kun få 2 som resultat.
Det er nemlig ikke muligt at tage kvadratroden (eller enhver anden lige rod) af et negativt tal, for der er ikke noget tal ganget med sig selv, der giver et negativt tal.

13
Et tal er enten et primtal eller et sammensat tal.
Tallet 1 er hverken et primtal eller et sammental. Det er et særligt tal, for det kan kun deles med sig selv.

Naturlige tal
Primtal
Sammensatte tal
Primtal
Et primtal er et helt positivt tal større end 1, der kun kan deles med 1 og tallet selv.
Fx kan tallet 3 kun deles med 1 og 3 og er derfor et primtal.
Primtal mellem 1 og 100

Sammensatte tal
Sammensatte tal er hele positive tal, der ikke er primtal.
De kan skrives som et gangestykke af primtal, f.eks. 6 = 2 x 3.
Sammensatte tal kan deles med flere end 2 tal.
EKS: 6 kan deles med 1, 2, 3 og 6.
14
Opløse i primfaktorer
Alle sammensatte tal kan opløses i primfaktorer dvs. skrives som et gangestykke af primtal.
METODE 1:


METODE 2:


Opløse i primfaktorer
15
Romerne brugte bogstaver til at skrive tallene med.

Regler:
Tegn, der skrives bagved et større, lægges til
Tegn, der står mellem to tegn, trækkes fra det
sidste og lægges til det første
Der må højst stå tre ens tegn efter hinanden
Tegn, der skrives foran et større, trækkes fra
Fx. lV = 5 - 1
Fx. Vl = 5 + 1
Fx. LlX = 50 + 10 - 1
Fx. XXX = 30
Store tal er skrevet sammen af flere mindre:
MCDLXXIX = M + CD + LXX + IX
1479 = 1000 + 400 + 70 + 9
Fx.
16
MAT håndbogen
17
7-9. kl
Hele tal, decimaltal, brøktal, procenttal, kvadrattal, kubiktal, primtal, negative tal, potenstal, rationale tal, irrationale tal